10. Result and Validation

10.1. Calculation of Total Weightage

Sum weightage for all the parameter classes to obtain the total weightage for each cell of the raster data. In order to do this, we need to reclassify the raster again according to the weightage.

Let us consider the weightage for slope we calculated in the last chapter.

##-------------
# Calculation of Weightage for Slope classes
##-------------
import pandas as pd
slopewt = pd.read_csv('../data/classstat/slopewt.csv')
slopewt.style.hide(axis="index")

Slope Class	Non-Landslide Area(m2)	Landslide Area(m2)	denseclas	densemap	weight
1	11055468.750000	0.000100	0.000000	0.000771	-18.260872
2	50358593.750000	15156.250000	0.000301	0.000771	-0.940908
3	43914531.250000	42812.500000	0.000974	0.000771	0.233759
4	4630781.250000	19687.500000	0.004233	0.000771	1.703165
5	93437.500000	7187.500000	0.071429	0.000771	4.528847

Weightage for slope class 1 = -18.260872

We reclassify all the slope class with value 1 to -18.260872.

To reclassify the slope class raster, we again create rules file slopewtrule.txt as follows:

1:1:-18.260872 etc

We can create all the rules file using the following python code.

##-------------
# Calculation of Rules for Different classes
##-------------
def writeWtRule(infile, outfile, cln):
# cln = class name
    cln = cln + " Class"
    wt = pd.read_csv(infile)
    df=open(outfile, 'w')
    for index, row in wt.iterrows():
        df.write(f"{row[cln]}:{row[cln]}:{row['weight']}\n")
#---Slope-------------
wtfile = '../data/classstat/slopewt.csv'
wtrulefile = '../data/classstat/slopewtrule.txt'
writeWtRule(wtfile, wtrulefile, "Slope")
#---Aspect------------
wtfile = '../data/classstat/aspwt.csv'
wtrulefile = '../data/classstat/aspwtrule.txt'
writeWtRule(wtfile, wtrulefile, "Aspect")
#---NDVI------------
wtfile = '../data/classstat/ndviwt.csv'
wtrulefile = '../data/classstat/ndviwtrule.txt'
writeWtRule(wtfile, wtrulefile, "NDVI")
#---NDWI------------
wtfile = '../data/classstat/ndwiwt.csv'
wtrulefile = '../data/classstat/ndwiwtrule.txt'
writeWtRule(wtfile, wtrulefile, "NDWI")
#---Profile Curvature------------
wtfile = '../data/classstat/profwt.csv'
wtrulefile = '../data/classstat/profwtrule.txt'
writeWtRule(wtfile, wtrulefile, "Profile Curvature")
#---Tangent Curvature------------
wtfile = '../data/classstat/tanwt.csv'
wtrulefile = '../data/classstat/tanwtrule.txt'
writeWtRule(wtfile, wtrulefile, "Tangent Curvature")
#---River Distance------------
wtfile = '../data/classstat/riverwt.csv'
wtrulefile = '../data/classstat/riverwtrule.txt'
writeWtRule(wtfile, wtrulefile, "River Distance")

In the similar way, we calculate rules for each parameters using r.recode as before. r.recode input=recl.slope@NewBasin output=wt.slope rules=path/to/slopewtrule.txt

After we reclassify all the raster-weightage file, we will find the sum.

Summation of all the raster-weightage file is simple. Use the following code:

r.series input=wt.slope,wt.aspect,wt.ndvi,wt.ndwi,wt.profcurv,wt.tancurv,wt.riverdist output=sumwt method=sum

Where each input corresponds to the weightage for each parameter and sumwt is the output raster.

Read the manual for r.series and you will find that it can be used to calculate various statistics from multiple rasters.

The summed weightage raster is shown in the following image.

Note

rivers are clipped to the extent of NewBasin using following code. v.select --overwrite ainput=river@PERMANENT binput=basin@PERMANENT btype=area output=riverclip operator=within

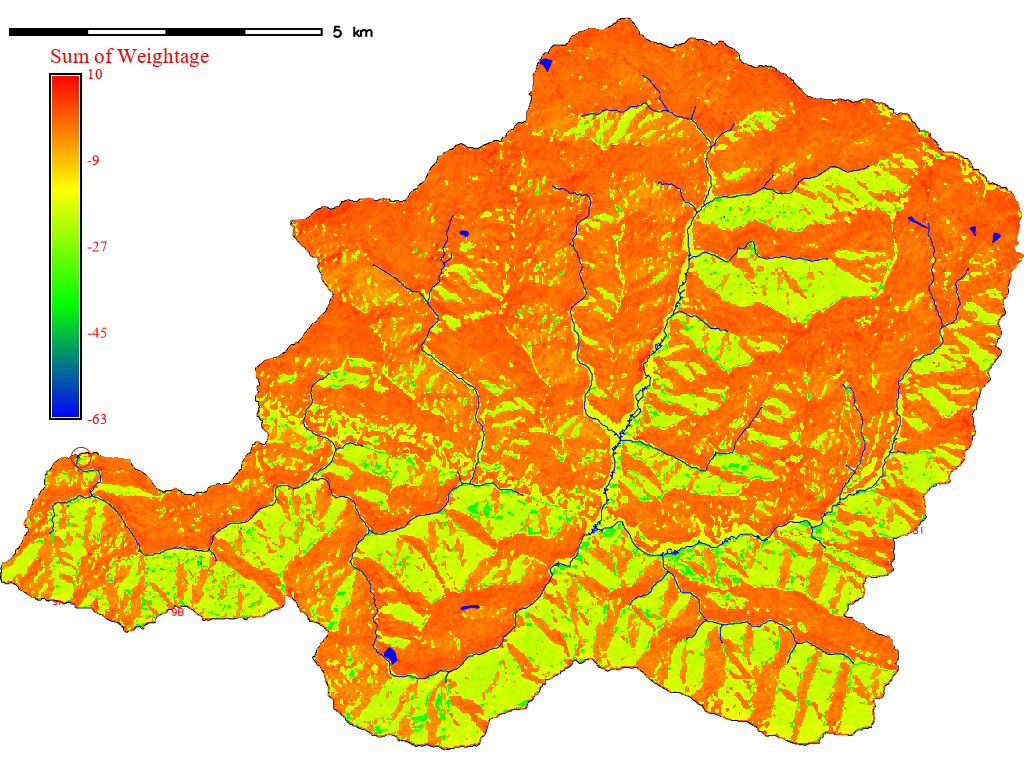
Fig. 10.1 Sum of weightage of all parameters

Beyond this, you will need personal judgement and some reading of references. However, it is always possible to refer to the same process as explained below.

Final product of landslide susceptibility analysis is a raster data classified into susceptibility ranges, e.g., high hazard, moderate hazard, low hazard etc. To do this we will follow the steps below:

1. Find the distribution of weightage (quantile), that is, area corresponding to each weightage range.

2. Reclassify the sum of weightage into these ranges.

3. Find the areas of landslide in each quantile ranges.

4. Find the success rate for prediction.

5. Select the boundary values for classifying the hazard level.

10.2. Distribution of sum-of-weight

Run the following code to find the distribution of weightage sum.

r.quantile -r input=sumwt quantiles=100 file=path/to/sumwtquantile.txt

The above code will distribute the range into 1% interval by area. The flag -r creates a rules file for reclassification. The output will be saved as sumwtquantile.txt.

-63.249979:-37.253528:1
-37.253528:-34.251851:2
-34.251851:-21.834766:3
-21.834766:-21.619461:4
-21.619461:-21.362525:5
-21.362525:-20.899584:6
-20.899584:-20.756630:7 and so on

The above quantile distribution means that sum of weightage from -63.25 to -37.25 occupies 1% of the whole area of the region and so on.

10.3. Reclassify the Weightage Sum

Use the rules file and use r.recode and the file created using r.quatile (path/to/sumwtquantile.txt) as rules file to reclassify the raster.

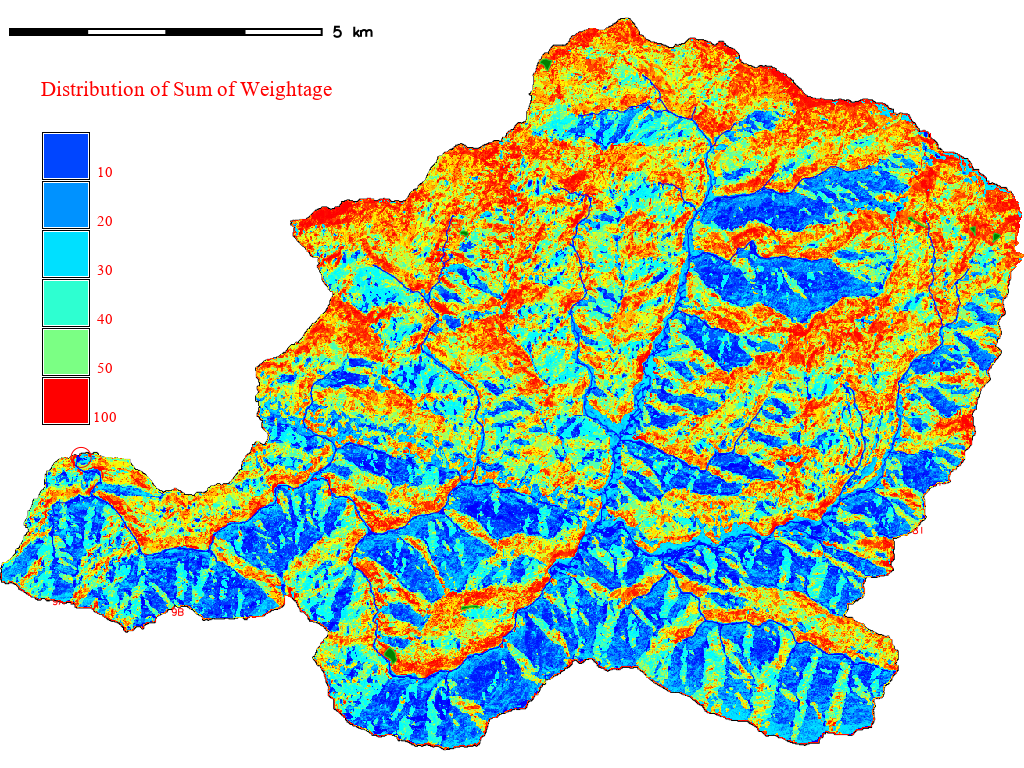
Fig. 10.2 Quantile Distribution of Sum of Weightage

10.4. Find the Area of Landslide in Each Quantile Range

Let us again use the r.stats code to to find the distribution of landslide in each range.

1. Code to calculate stats: r.stats -a input=wtqantile,lsrast output=path/to/sumwtcross.csv separator=, null_value=-1

2. Use following python code to read sumwtcross.csv

##-------------
# Sum of weight classified and cross-tabulation
##-------------
filename = '../data/classstat/sumwtcross.csv'
wt = pd.read_csv(filename, header=None)
wt.columns = ["Percentile", 'Landslide/No landslide', 'Area(m2)']
wt = wt[wt["Percentile"] > 0]
display(wt.head(10))
display(wt.tail(10))

	Percentile	Landslide/No landslide	Area(m2)
0	1	-1	1111562.50
1	2	-1	1108906.25
2	3	-1	1057031.25
3	4	-1	1156406.25
4	5	-1	1046093.75
5	6	-1	1181562.50
6	7	-1	979375.00
7	8	-1	1196250.00
8	9	-1	1142187.50
9	10	-1	947968.75

	Percentile	Landslide/No landslide	Area(m2)
137	96	1	3593.75
138	96	-1	1053593.75
139	97	1	4375.00
140	97	-1	1205000.00
141	98	1	7812.50
142	98	-1	1071718.75
143	99	1	7656.25
144	99	-1	1099218.75
145	100	1	29375.00
146	100	-1	1080937.50

10.5. Find the success rate

Success rate of the sum of weightage is determined by how many percentage of landslide are predicted by the highest sum of weightage. Let us see the area of landslide within each of the top sum-of-weightage class.

We use python code to find the percentile-wise cumulative landslide area. For this we need to:

1. Remove the rows with no landslide

2. Reverse the table

3. Calculate cumulative percentile

##-------------
# Area - reverse
##-------------
wt = wt[wt["Landslide/No landslide"] > 0]
lsarea = 8.48438e+04
wt.insert(3,"pc",0)
#print(wtrev.head())
wt['pc'] = wt['Area(m2)'].apply(lambda x: float(x)*100.0/lsarea)
wtrev = wt.reindex(index=wt.index[::-1])
wtrev['pcsum'] = wtrev['pc'].cumsum()
wtrev['Percentile'] = wtrev['Percentile'].apply(lambda x: 101-x)
display(wtrev.head(10))

	Percentile	Landslide/No landslide	Area(m2)	pc	pcsum
145	1	1	29375.00	34.622447	34.622447
143	2	1	7656.25	9.023936	43.646383
141	3	1	7812.50	9.208098	52.854481
139	4	1	4375.00	5.156535	58.011016
137	5	1	3593.75	4.235725	62.246740
135	6	1	4687.50	5.524859	67.771599
133	7	1	2656.25	3.130753	70.902352
131	8	1	1718.75	2.025781	72.928134
129	9	1	1875.00	2.209943	75.138077
127	10	1	1875.00	2.209943	77.348021

Above table shows the cumulative area of landslide within each percentile starting from highest weightage. We can see that area of landslide within top 1% of the pixels = \(29375.00 m^2\), which is about 34% of the total area. Similarly, area of landslide within top 2% is about 43%. Plotting the values of cumulative landslide area with respect to the percentile will give us the idea of success rate of the susceptibility map. We can plot graph using python library called plotly.

##-------------
# Roc Curve
##-------------
import plotly.express as px

fig = px.line(wtrev, x="Percentile", y="pcsum", title='Success Rate of Prediction')
fig = px.line(wtrev, x="Percentile", y="pcsum", 
labels={
                     "Percentile": "Percentage map",
                     "pcsum": "Cumulative Sum of Percentage of Landslide area"
                 },
                 title='Success Rate of Prediction')



fig.update_layout(
    autosize=False,
    width=800,
    height=600,
    margin=dict(
        l=50,
        r=50,
        b=100,
        t=100,
        pad=4
    ),
    paper_bgcolor="LightSteelBlue",
)
fig.update_traces(line_color='#aa0000', line_width=1)
##fig.write_image('path/to/image) # Uncomment this line to produce image
fig

10.6. Select the Boundary Value for Hazard Zone

We can observe following points from the above graph:

1. About 90% of landslides occur in the top 20 percentiles.

2. About 100% of landslides occur in the 50 percentiles.

3. Bottom (Lowest sum-of-weightage) 50% has almost no landslide.

We will chose the boundaries between three hazard zones and reclassify the quantile raster again into landslide classes using the following rule:

Rules text hazard zonation

1:50:1
51:80:2
81:100:3

Label the newly classified raster map as

1 - Low
2 - Moderate
3 - High

Where 1, 2 and 3 represent low, moderate and high hazard respectively.

With this we get the final susceptibility map.

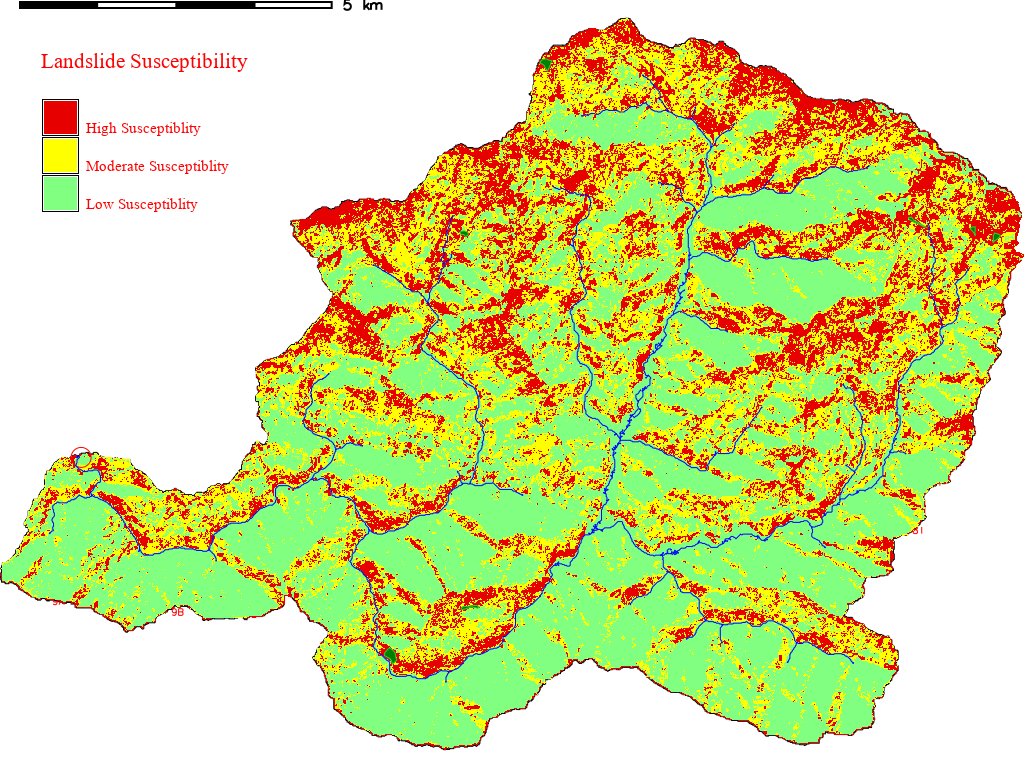
Fig. 10.3 Landslide Susceptibility Map